top of page
Sukhjeet Singh
Sep 21, 20226 min read

Homomorphic Encryption Keeps Your Data Encrypted All Time

What is Homomorphic Encryption?

The term "homomorphic" in mathematics refers to the translation of one collection of data into another while maintaining the connections between the components in both sets. The phrase has Greek roots that mean "similar structure." Since the data structure is preserved in a homomorphic encryption system, the same mathematical operations on encrypted or decrypted data will produce equal results. Most homomorphic encryption techniques actually perform best when data is represented as an integer and addition and multiplication are used as the operational operations. This indicates that without actually decrypting the data, it can be altered and examined as though it were in plaintext format. Only you can decrypt the ciphertext and understand what it means, even though the encrypted data can be computed and processed to generate an encrypted answer.


Homomorphic encryption was created to enable computation on encrypted data. As a result, data can stay private while being processed, allowing for the completion of useful activities using information from unreliable environments. This is incredibly useful in a world of distributed computation and heterogeneous networking. Like other types of public encryption, a homomorphic cryptosystem encrypts data using a public key and restricts access to its decrypted contents to those with the corresponding matching private key. Its use of an algebraic structure enables a range of computations (or operations) on the encrypted data, however, distinguishes it from other types of encryptions. The use of algebraic structure also safeguards it from quantum computers.

5 Step Process for Homomorphic Encryption

The use of homomorphic encryption to encrypt any data involves five-stage processing, which is as follows:


1. Setup

The setup stage involves three steps:

  • Choose an appropriate scheme to apply

  • Deciding on security parameters

  • Choosing functional parameters

2. Key Generation

  1. Public Key

  2. Re-Linearization Key

  3. Galois Key

Only the public key can be used for the encryption of these three keys. All of these keys (including the public keys) can be shared with external entities and can also be used for computational results.


3. Encryption

Input

A number or vector of numbers

​Output

A cipher text which is two N-degree polynomials

4. Evaluation

The encryption text must undergo certain processes. This process will likewise produce a cipher text as its result.


5. Decryption

Cipher text decryption utilizes a secret key to restore the desired outcome.


Application Areas - Homomorphic Encryption

Homomorphic encryption is significant because it enables calculations on encrypted data. It is impossible to retrieve the original data without the correct decryption key. This implies that data processing can be delegated to a third party without having faith in the data's security. The capacity to process encrypted data has the potential to address several significant business issues encountered by businesses in all sectors. Following are some key application areas where homomorphic encryption is used:


1. Supply Chain Security - The majority of businesses rely on reliable third parties for various aspects of their operations. To perform their duties, these vendors, contractors, and other third parties frequently need access to confidential and sensitive company information. The dangers of insecure supply chains have been highlighted by recent incidents, which also show how hackers would aim for the weakest link in the chain to accomplish their goals. This means that giving a partner access to sensitive data could expose a company to a costly and harmful data breach. A business can help protect itself against these supply chain dangers by using homomorphic encryption. A data breach provides no harm to the organization if all data given to reputable third parties for processing is encrypted. This reduces the risk associated with outsourcing key data processing for an organization.


2. Regulatory Compliance - The legislative environment for data protection has become more complicated in recent years. New laws, including the EU's Data Protection Regulation (GDPR), have given individuals new rights while also imposing new obligations and limitations on enterprises. The GDPR rule requiring that EU residents' data remain inside the EU or in nations or organizations with equal data security standards is one that many firms are having trouble complying with. One of the primary GDPR justifications for data flows between the EU and the US was rejected by the Schrems II judgment in 2020, which generated issues for many US companies who do business with EU citizens. The provisions of laws like the GDPR are expressly stated not to apply to encrypted data. A business might possibly store and process data using homomorphic encryption outside the EU and only decode it on servers in regions that adhere to GDPR regulations.


3. Private Data Analytics - Many businesses rely on data analytics to generate revenue. By gathering user data, analyzing it, and then selling it to other parties for targeted advertising, companies like Facebook are able to offer "free" services. The monetization of personal data is debatable, though. Many consumers are upset that businesses are creating detailed profiles of them without giving them any visibility or control over the information being gathered and used. To address this issue, homomorphic encryption offers a viable solution. A business such as Facebook may use homomorphic encryption to execute the necessary data analyses without having access to or the capacity to view the original data. Users having access to the encryption keys opens the door to the possibility of targeted, private advertising.


Open-Source Implementations

Homomorphic encryption techniques have numerous open-source implementations available today. Following is a list of some of them:

  • Microsoft SEAL: A widely used open-source library from Microsoft that supports the BFV and the CKKS schemes.

  • PALISADE: A widely-used open-source library from a consortium of DARPA-funded defense contractors that supports multiple homomorphic encryption schemes such as BGV, BFV, CKKS, TFHE, and FHEW, among others, with multiparty support.

  • HELib: An early and widely used library from IBM that supports the CKKS and BGV scheme and bootstrapping.

  • FHEW / TFHE: Supports the TFHE scheme. (Please note that the FHEW and TFHE libraries are distinct from the FHEW and TFHE schemes which are also supported by other libraries listed on this page.)

  • HeaAn: This library implements the CKKS scheme with native support for fixed point approximate arithmetic.

  • Λ ○ λ (pronounced “L O L”): This is a Haskell library for ring-based lattice cryptography that supports FHE.

  • NFLlib: This library is an outgrowth of the European HEAT project to explore high-performance homomorphic encryption using low-level processor primitives.

  • HEAT: This library focuses on an API that bridges FV-NFLib and HeLIB.

  • cuHE: This library explores the use of GPGPUs to accelerate homomorphic encryption.

  • Lattigo: This is a lattice-based cryptographic library written in Go.

  • Concrete: This library supports a custom variant of the TFHE scheme.

  • EVA: A compiler and optimizer for the CKKS scheme (targeting Microsoft SEAL).

Patent Data

Every day new technologies are emerging, and along with that, patent applications are also rising. Every inventor wants to safeguard their inventive ideas so as to keep them safe from competitors or from being misused. Having said that, there are already, 5323 patents being granted for homomorphic encryption technology.

Alipay Information Technology is leading the race with the maximum number of patent families, i.e., 233 in homomorphic encryption technology, followed by Shenzhen Qianhai Webank with 140 patents and then Advanced New Technologies with 127 patents. Besides these top three companies, Microsoft and IBM are also in the race to as data privacy and protection become a greater concern and companies are employing advanced encryption techniques such as holomorphic encryption.

The above-provided graph describes the geographical distribution of the patents related to homomorphic encryption technology. China is leading the race with 3478 patent families, followed by the USA with 1274 patent families, and then European Patent Office (EP) with 820 patent families.

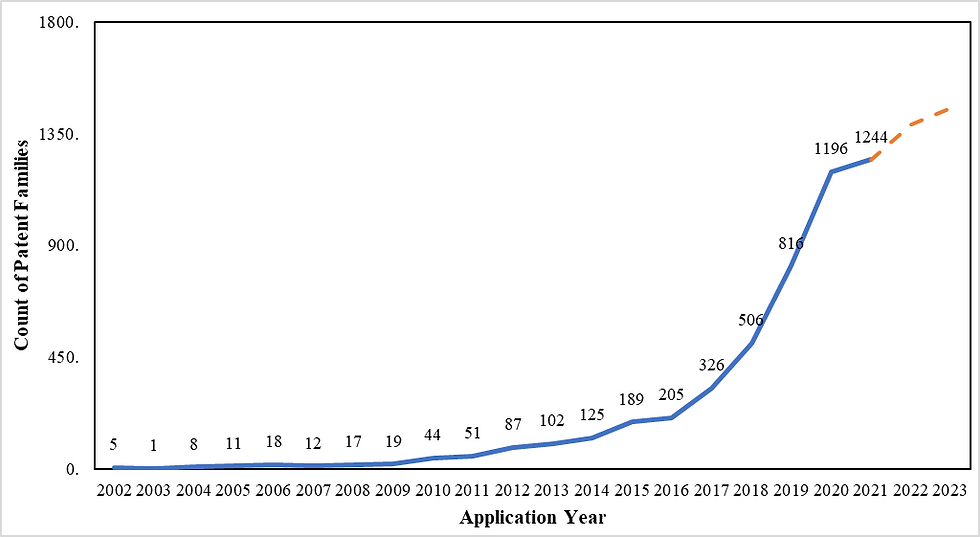
Homographic encryption as a concept was known since 1978 until Dr. Craig Gentry made the first system in 2009. The above-provided graph shows the trend of application filing regarding homomorphic encryption technology. It can be observed that a maximum patent was filed in the year 2021, i.e., 1244 patent applications, and a minimum in 2012, i.e., only 87 patent applications. An exponential increase in the number of filed patent applications is evident from the fact that excessive research on making the technology progressive started after the first breakthrough via Dr. Gentry.


Conclusion

Homomorphic encryption is being advanced by some of the biggest technological companies in the world to make it more accessible and user-friendly. For instance, SEAL (Simple Encrypted Arithmetic Library) is a collection of encryption libraries developed by Microsoft that enables computations to be carried out directly on encrypted data. Microsoft's SEAL team is working with businesses like IXUP to provide end-to-end encrypted data storage and compute services, which are powered by open-source homomorphic encryption technology. Businesses can use SEAL to build platforms for data analytics on data that is still encrypted, and the data owners never have to provide their encryption key to anybody else.


Google also unveiled its open-source cryptography tool, Private Join and Compute, as a further indication of its support for homomorphic encryption. Google's tool aims to analyze data in its encrypted form while making only the conclusions drawn from the analysis and not the underlying data itself available.


IBM also released the initial version of their HElib C++ library in 2016 with the intention of making homomorphic encryption more widely used. However, it is apparently "running 100 trillion times slower than plaintext operations." Since then, IBM has worked to address this problem, developing a version that is 75 times faster but still falls short of plaintext operations. Though homomorphic encryption is not fully feasible to be applied to each and every application area due to its limitations, but it is evident from history that researchers can make anything possible. So, looking at its practical applications, I think we are going to see homomorphic encryption slowly taking part in our daily lives in a short period of time.

References

Comments

bottom of page